Permutación circular demostración sección $\S 9$.

 Comenzamos nuestras notas para poder entender un poco mejor el libro de Mecánica de Landau, en esta ocasión nos trasladamos a la demostración del momento angular en la sección $\S 9$

Enseguida escribiré de forma muy ligera la demostración que se lleva a cabo en color negro, de acuerdo al libro, con unas breves frases que resumen el proceso, y cuándo lleguemos a la permutación circular, les mostrare cómo es posible realizar dicho proceso con una pequeña demostración:

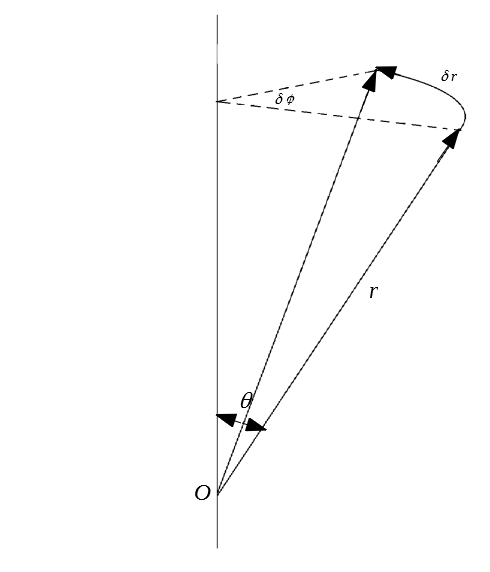
La magnitud de $|\delta r|$ de acuerdo a la imagen es:

$$|\delta\mathbf{r}|=rsen\theta \delta\phi$$

Esto se puede expresar cómo un producto vectorial:

$$\delta \mathbf{r}=\delta\boldsymbol{\phi}\times \mathbf{r}$$

Y su derivada respecto al tiempo:

$$\delta \mathbf{v}=\delta\boldsymbol{\phi}\times \mathbf{v}$$

Llevando las anteriores expresiones a la condición que el lagrangiano no varía por la rotación:

$$\delta L=\sum_a\left(\frac{\partial L}{\partial \mathbf{r}_a}\cdot \delta \mathbf{r}_a + \frac{\partial L}{\partial \mathbf{v}_a}\cdot \delta \mathbf{v}_a\right)=0$$

Sustituyendo de acuerdo a las definiciones que se obtienen directamente de las ecuaciones de Euler-Lagrange y las anteriores igualdades:

$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{r}_a}\right)=\frac{\partial L}{\partial r_a}$$

$$\frac{\partial L}{\partial \mathbf{v}_a}=\mathbf{p}_a \qquad \frac{\partial L}{\partial \mathbf{r}_a}=\dot{\mathbf{p}}_a$$

Obtenemos:

$$\delta L=\sum_a\left(\dot{\mathbf{p}}_a\cdot \delta\boldsymbol{\phi}\times \mathbf{r}_a + \mathbf{p}_a\cdot \delta\boldsymbol{\phi}\times \mathbf{v}_a\right)=0$$

En dónde mediante la permutación circular debemos sacar el factor $\delta\boldsymbol{\phi}$.

En este caso voy a demostrar lo siguiente: 

Dados tres vectores cualesquiera $\mathbf{A}$, $\mathbf{B}$ y $\mathbf{C}$:

$$\mathbf{A}=a_1i+a_2j+a_3k$$

$$\mathbf{B}=b_1i+b_2j+b_3k$$

$$\mathbf{C}=c_1i+c_2j+c_3k$$

Se cumple que:

$$A\cdot(B\times C)=C\cdot(A\times B)=B\cdot(C\times A)$$

Con:

$$\mathbf{A}\times\mathbf{B}=\begin{vmatrix}i & j & k\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\end{vmatrix}=\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix}i+\begin{vmatrix}a_3 & a_1\\ b_3 & b_1\end{vmatrix}j+\begin{vmatrix}a_1 & a_2\\ b_1 & b_2\end{vmatrix}k$$

$$\mathbf{A}\times\mathbf{B}=(a_2b_3-b_2a_3)i+(a_3b_1-b_3a_1)j+(a_1b_2-b_1a_2)k$$

Por lo tanto si aplicamos el producto punto ($\cdot$) al vector resultante del producto cruz obtenemos el escalar:

$$C\cdot(\mathbf{A}\times\mathbf{B})=[c_1i+c_2j+c_3k]\cdot[(a_2b_3-b_2a_3)i+(a_3b_1-b_3a_1)j+(a_1b_2-b_1a_2)k]$$

$$C\cdot(\mathbf{A}\times\mathbf{B})=(a_2b_3-b_2a_3)c_1+(a_3b_1-b_3a_1)c_2+(a_1b_2-b_1a_2)c_3$$

$$C\cdot(\mathbf{A}\times\mathbf{B})=a_2b_3c_1-b_2a_3c_1+a_3b_1c_2-b_3a_1c_2+a_1b_2c_3-b_1a_2c_3$$

Si factorizamos respecto a $a_1$, $a_2$ y $a_3$ obtenemos $\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})$
$$C\cdot(\mathbf{A}\times\mathbf{B})=(b_2c_3-c_2b_3)a_1+(b_3c_1-c_3b_1)a_2+(b_1c_2-c_1b_2)a_3=\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})$$

Siguiendo el mismo procedimiento factorizando respecto a $a_1$, $a_2$ y $a_3$ obtenemos $\mathbf{B}\cdot(\mathbf{C}\times\mathbf{A})$

Luego volviendo a nuestra demostración, por esta propiedad es posible expresar:

$$\dot{\mathbf{p}_a}\cdot\delta \boldsymbol{\phi}\times \mathbf{r}_a=\delta \boldsymbol{\phi}\cdot\mathbf{r}_a \times\dot{\mathbf{p}_a} \qquad\mathbf{p}_a\cdot\delta \boldsymbol{\phi}\times \mathbf{v}_a=\delta \boldsymbol{\phi}\cdot\mathbf{v}_a \times\mathbf{p}_a$$

Reemplazamos las expresiones anteriores en la variación del lagrangiano y tenemos:

$$\sum_a(\delta \boldsymbol{\phi}\cdot\mathbf{r}_a \times\dot{\mathbf{p}_a}+\delta \boldsymbol{\phi}\cdot\mathbf{v}_a \times\mathbf{p}_a)$$

Factorizamos $\delta \boldsymbol{\phi}$ y obtenemos:

$$\delta \boldsymbol{\phi}\cdot\sum_a(\mathbf{r}_a \times\dot{\mathbf{p}_a}+\mathbf{v}_a \times\mathbf{p}_a)$$

El parentesis es la derivada de un producto:

$$\delta \boldsymbol{\phi}\cdot\frac{d}{dt}\sum_a \mathbf{r}_a\times \mathbf{p}_a=0$$

Puesto que $\delta \boldsymbol{\phi}$ es arbitrario, resulta:

$$\frac{d}{dt}\sum_a \mathbf{r}_a\times \mathbf{p}_a=0$$

Luego se concluye que en el movimiento de un sistema cerrado se conserva la magnitud vectorial:

$$M\equiv\sum_a \mathbf{r}_a\times \mathbf{p}_a$$

La cuál es el momento angular (o momento cinético) del sistema.

Sí conoces otra forma de demostrar la permutación circular, no dudes de colocarlo en los comentarios, si necesitas colocar ecuaciones puedes utilizar lenguaje latex entre $\setminus[$ y $\setminus]$.