Campo debido a dos puntos Capítulo 2

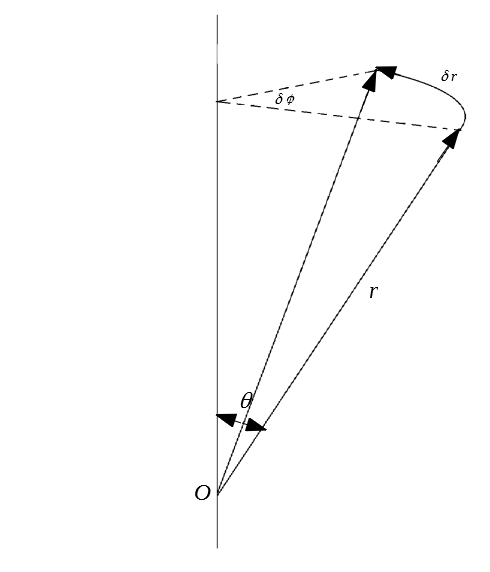
Los siguientes problemas van a estar dedicados uno a uno en diferente página para evitar demasiado texto y corresponde a los presentes después de la sección $\S 9$: 3. Indicar las componentes del ímpetu $\mathbf{p}$ y del momento cinético $\mathbf{M}$ que se conservan en un movimiento dentro de los siguientes campos: d) Campo debido a dos puntos. La forma mas fácil de representar un campo debido a dos puntos es mediante coordenadas esféricas, teniendo en cuenta que pueden variar los ángulos y el radio (esto debido a que no se especifica que clase de campo puede existir entre los dos puntos), resulta bastante práctico para este caso: Su lagrangiano expresado en coordenadas rectangulares es: \[L=\frac{1}{2}m(\dot{x}^2+\dot{y}^2+\dot{z}^2)-U(\mathbf{r_1},\mathbf{r_2},...)\] Utilizando la transformación de coordenadas rectangulares a coordenadas esféricas: \[x=rsen\theta cos\phi \qquad y=rsen\theta sen\phi \qquad z=rcos\theta\] Y sus derivadas respecto al tiempo: \[\dot{x}=\dot{r}sen\...